Figure 2 - P-8250115

INTERCEPT PROCEDURES TEXTBOOK

Figure 2

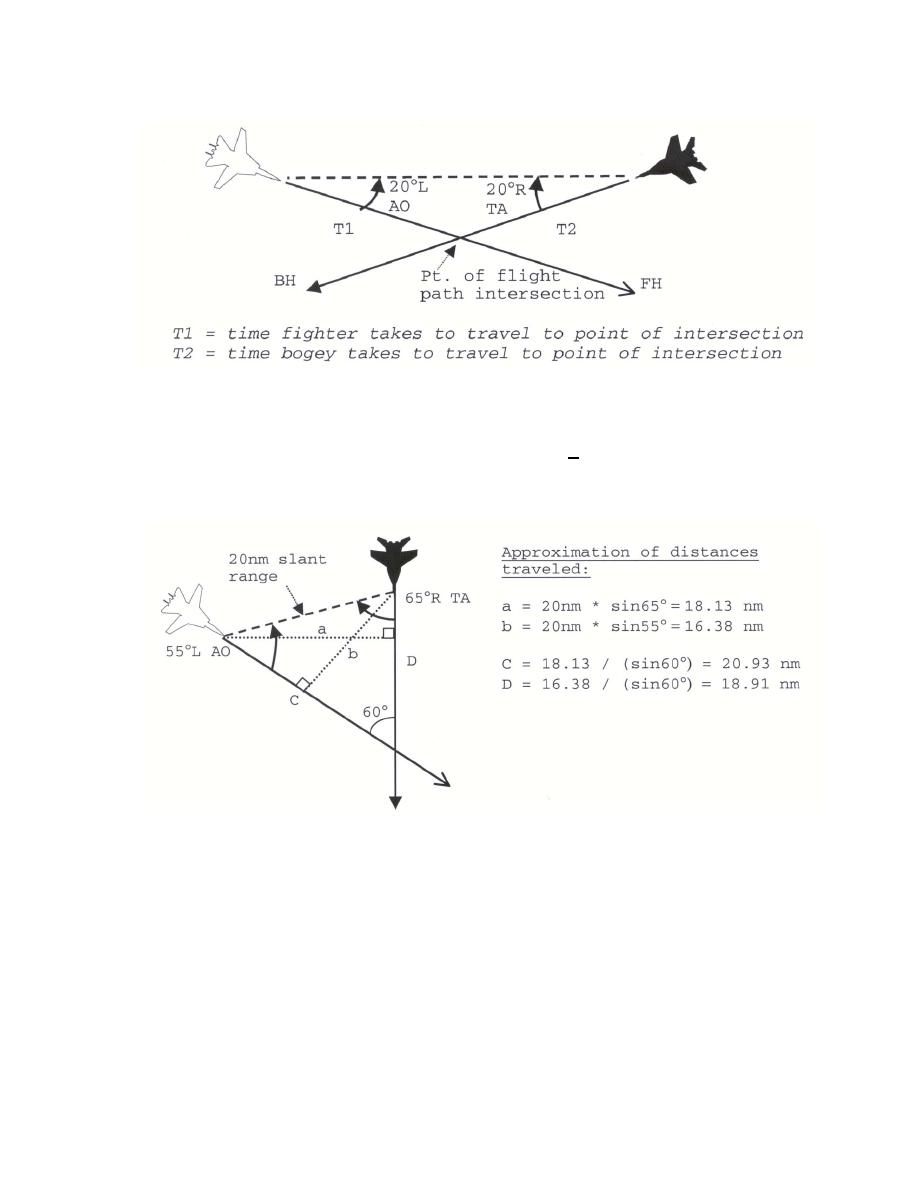
The figure below shows the approximate flight path distance of both aircraft when TA is

65R and the bogey is within the functional limits of the scope (+55). The actual flight path

distance computation would involve trigonometric relationships not relevant to practical

execution. The computations below are provided for illustration purposes.

Figure 3

In this example, a conventional collision course correction of "Right hard 10, steady _____"

would place the bogey outside the scope limits at 65L. However, the bogey has a shorter

distance to travel than the fighter. So if the fighter takes no action, the bogey will drift across the

fighter's nose.

The fighter in this case must cover approximately 20.93 nm in the same time the bogey

travels approximately 18.91 nm. To do this, the fighter must increase airspeed. How much of an

increase is determined by complex mathematical formulas. Without going through all of the

math, here at VT-86 the required speed advantage for these high TA intercepts will be .1 IMN

over the bogey's airspeed.

109